首先本OJ的rating系统已经完全修复完成了。
今天晚上对着一份本来就没有任何对的意思的代码，调了半天，怎么每次计算都是错的呢，怎么第一名The__Flash一直都是rating下降最多的，而后面的反而又升高了呢。
实际上是之前的算法理解错了，现在正式详细解读并且公开本OJ的rating算法。
首先本OJ的Rating算法是基于Codeforces的ELO算法。
首先我们定义一个变量:
P_{i,j}=\frac{1}{1+10^{\frac{r_j-r_i}{400}}}
这个变量代表的是选手i能够胜出选手j的概率，也就是说如果选手j的rating r_j比选手i的ratingr_i大很多的话，那么这个数就会越来越小也就是说选手i的胜率也会越来越小
有了这个变量之后我们需要计算每次比赛之前选手i应该期望的名次:

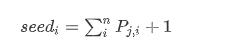
如果当前选手未定级那么
seed_i=1+\frac{n}{2} n为总计算rating人数 我们读取比赛结束后当前选手的排名rank_i取几何平均数m_i=\sqrt{rank_i\times seed_i}
这样我们得出了当前比赛结束后这位选手的期望排名
接下来我们需要二分一个seed_j使得seed_j=m_i我们拿比赛之后变化的ratingr_j作为变量，最终我们会得到一个新的ratingr_j然后定义del_i=\frac{r_j-r_i}{2}这样我们得到了初试的rating变化
这里二分实际上是很好说明他的单调性的首先10^x是一个指数函数那么他是单调递增的函数10^{-x}是单调递减的函数，那么
\frac{1}{1+10^{\frac{r_j-r_i}{400}}} 显然当我们的400上面的分子左边的二分r_j大的时候我们对应的要找的seed_j就会变小，反之就会变大，这样经过浮点数二分就可以找到一个基本符合的r_j使得seed_j=m_i
接下来我们需要两次微调
第一次微调是使得所有选手的rating不会太过膨胀(inflation)
我们取所有人的del_i的加和也就是\sum del_i然后定义第一个dec量为
dec=\frac{-1-\sum del_i}{n} n为当前计算rating的总人数
之后我们让所有人的
del_i+=dec
这就完成了第一次微调
第二次微调是为了让那些前几名的rating选手rating增长的不会过于垄断，也就是rating高的越高这种情况发生
取前m=min(n,4\sqrt{n})名选手，使得他们的rating继续下降，下降的值为
dec=min(max(-10,\frac{-\sum del_i}{m}),0)
这样经过总共的两次微调最终的rating就会显现给大家了

--马鸿儒