题目描述

Alice and Bob are playing a game on a matrix, consisting of $2$ rows and $m$ columns. The cell in the $i$-th row in the $j$-th column contains $a_{i,j}$ coins in it.

Initially, both Alice and Bob are standing in a cell $(1,1)$. They are going to perform a sequence of moves to reach a cell $(2,m)$.

The possible moves are:

• Move right — from some cell $(x,y)$ to $(x,y+1)$;
• Move down — from some cell $(x,y)$ to $(x+1,y)$.

First, Alice makes all her moves until she reaches $(2,m)$. She collects the coins in all cells she visit (including the starting cell).

When Alice finishes, Bob starts his journey. He also performs the moves to reach $(2,m)$ and collects the coins in all cells that he visited, but Alice didn't.

The score of the game is the total number of coins Bob collects.

Alice wants to minimize the score. Bob wants to maximize the score. What will the score of the game be if both players play optimally?

输入格式

The first line contains a single integer $t (1≤t≤10^4)$ — the number of testcases.

Then the descriptions of t testcases follow.

The first line of the testcase contains a single integer $m$ $(1≤m≤10^5)$ — the number of columns of the matrix.

The i-th of the next 2 lines contain m integers a_{i,1},a_{i,2},…,a_{i,m} $(1≤ai,j≤10^4)$ — the number of coins in the cell in the i-th row in the j-th column of the matrix.

The sum of m over all testcases doesn't exceed $10^5$.

输出格式

For each testcase print a single integer — the score of the game if both players play optimally.

样例

3 
3 
1 3 7 
3 5 1 
3 
1 3 9 
3 5 1 
1 
4 
7 

7 
8 
0 

提示

The paths for the testcases are shown on the following pictures. Alice's path is depicted in red and Bob's path is depicted in blue.

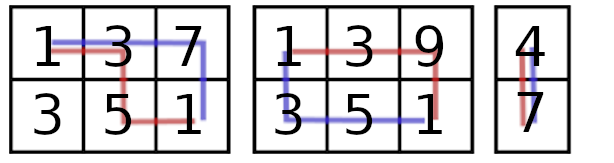
By QLU_ZenF1sh