#P2582. 耳听怒
耳听怒
题目背景
"千里黄风万里沙,八百方圆无人家。半妖半仙谁评说,是盗是圣何足挂。"
题目描述
黄风大圣不愿与你争斗,于是他与你玩了一个小游戏。
现在有一个由 个小正方形组成的网格图,其中每个小正方形的边长为 ,"你" 和 "黄风大圣" 在这上面进行一场染色游戏,游戏的规则如下:
"你" 和 "黄风大圣" 轮流进行操作,"黄风大圣" 先手。
当轮到 "黄风大圣" 操作时,他可以选择一条尚未被染色的正方形边框并将其染成红色。操作结束时,如果这条边框是一个(或两个)正方形最后一条被染色的边框,则自动将该正方形也同样染成红色。
当轮到 "你" 操作时,你可以选择一条尚未被染色的正方形边框并将其染成蓝色。操作结束时,如果这条边框是一个(或两个)正方形最后一条被染色的边框,则自动将该正方形也同样染成蓝色。
当所有的边框都被染色后,游戏结束。此时染成自己所属颜色的正方形数量更多的一方获胜;或者当数量相等时,达成平局。 已知网格图的边长 ,如果两人都按照最优策略,尽可能地让自己获胜,或者在自己无法获胜的前提下尽可能地达成平局,请你推断哪一方会获胜或达成平局。
例如,在 的网格图中,一种可能的游戏过程如下:
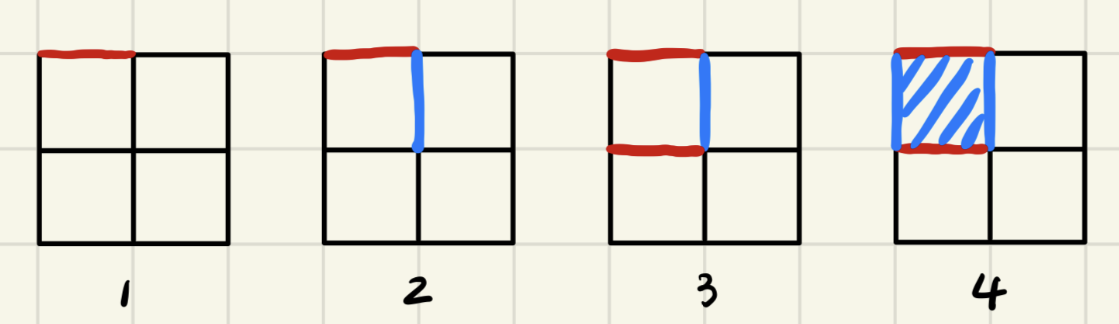
输入格式
一行包含一个整数 表示网格边长 。
输出格式
如果 "你" 获胜,输出 Tianmingren; 如果 "黄风大圣" 获胜,输出Huang; 如果平局输出 Ping。
样例
1
Tianmingren
相关
在下列比赛中:
